Stack manipulation
In this section we describe the AIR constraints for Miden VM stack manipulation operations.
PAD¶
The PAD operation pushes a \(0\) onto the stack. The diagram below illustrates this graphically.
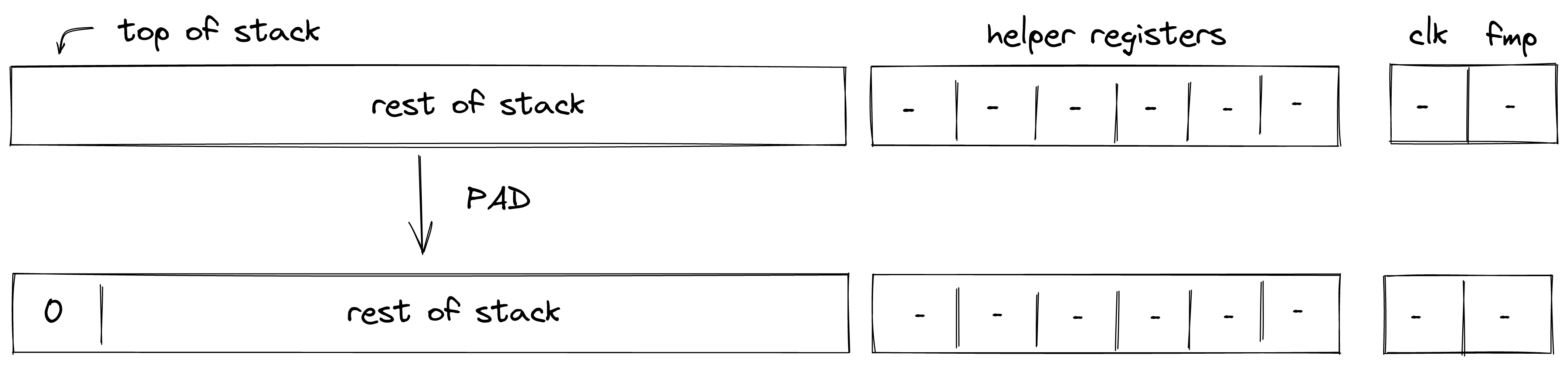
Stack transition for this operation must satisfy the following constraints:
\[ s_{0}' = 0 \text{ | degree} = 1 \]
The effect of this operation on the rest of the stack is:
- Right shift starting from position \(0\).
DROP¶
The DROP operation removes an element from the top of the stack. The diagram below illustrates this graphically.
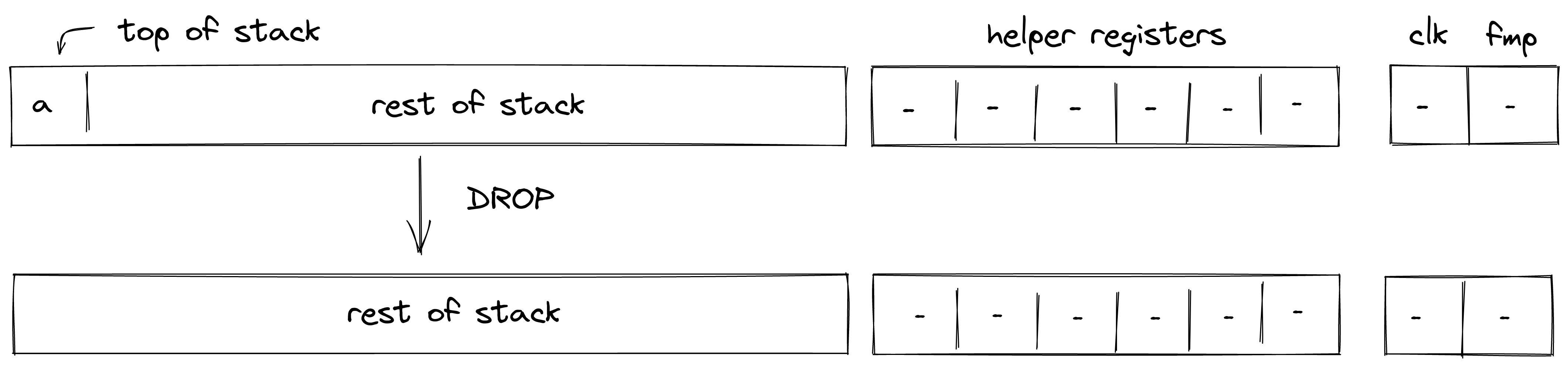
The DROP operation shifts the stack by \(1\) element to the left, but does not impose any additional constraints. The degree of left shift constraints is \(1\).
The effect of this operation on the rest of the stack is:
- Left shift starting from position \(1\).
DUP(n)¶
The DUP(n) operations push a copy of the \(n\)-th stack element onto the stack. Eg. DUP (same as DUP0) pushes a copy of the top stack element onto the stack. Similarly, DUP5 pushes a copy of the \(6\)-th stack element onto the stack. This operation is valid for \(n \in \{0, ..., 7, 9, 11, 13, 15\}\). The diagram below illustrates this graphically.
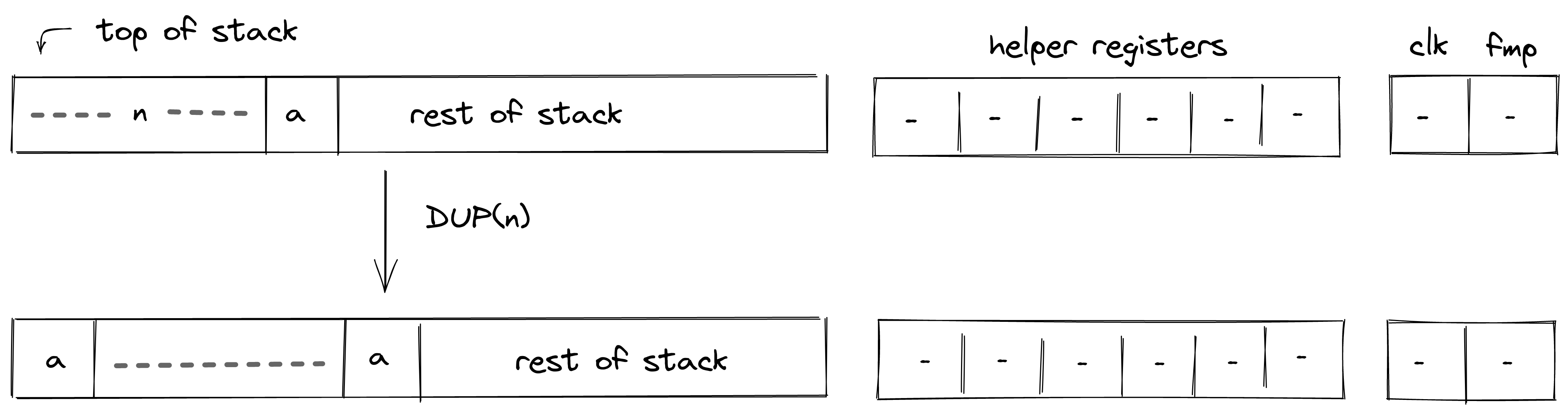
Stack transition for this operation must satisfy the following constraints:
\[ s_{0}' - s_{n} = 0 \text{ for } n \in \{0, ..., 7, 9, 11, 13, 15\} \text{ | degree} = 1 \]
where \(n\) is the depth of the stack from where the element has been copied.
The effect of this operation on the rest of the stack is:
- Right shift starting from position \(0\).
SWAP¶
The SWAP operations swaps the top two elements of the stack. The diagram below illustrates this graphically.
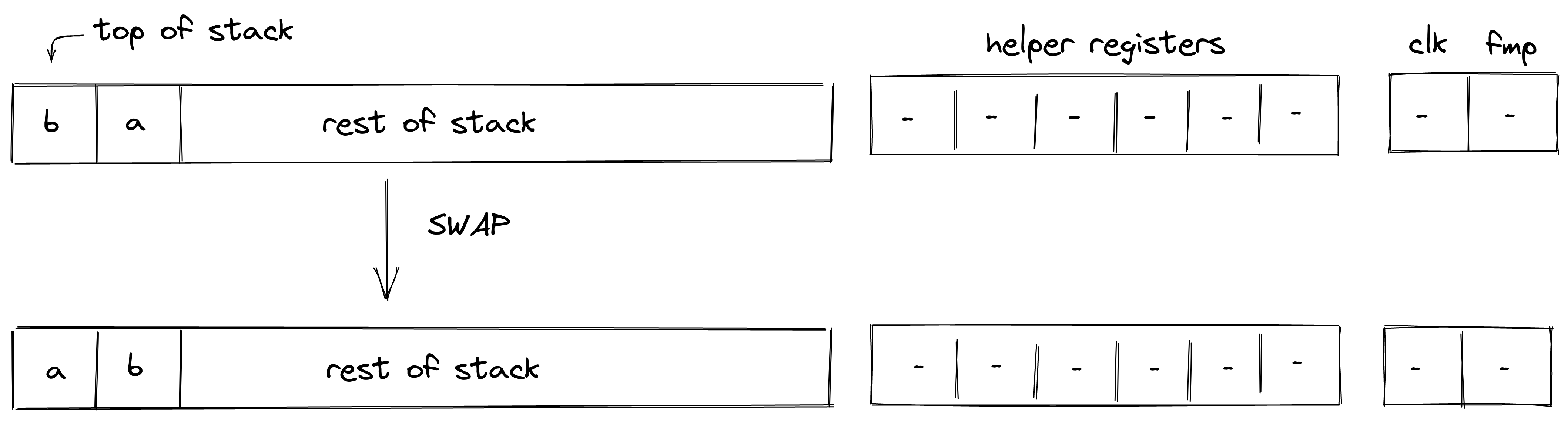
Stack transition for this operation must satisfy the following constraints:
\[ s_{0}' - s_{1} = 0 \text{ | degree} = 1 \]\[ s_{1}' - s_{0} = 0 \text{ | degree} = 1 \]
The effect of this operation on the rest of the stack is:
- No change starting from position \(2\).
SWAPW¶
The SWAPW operation swaps stack elements \(0, 1, 2, 3\) with elements \(4, 5, 6, 7\). The diagram below illustrates this graphically.
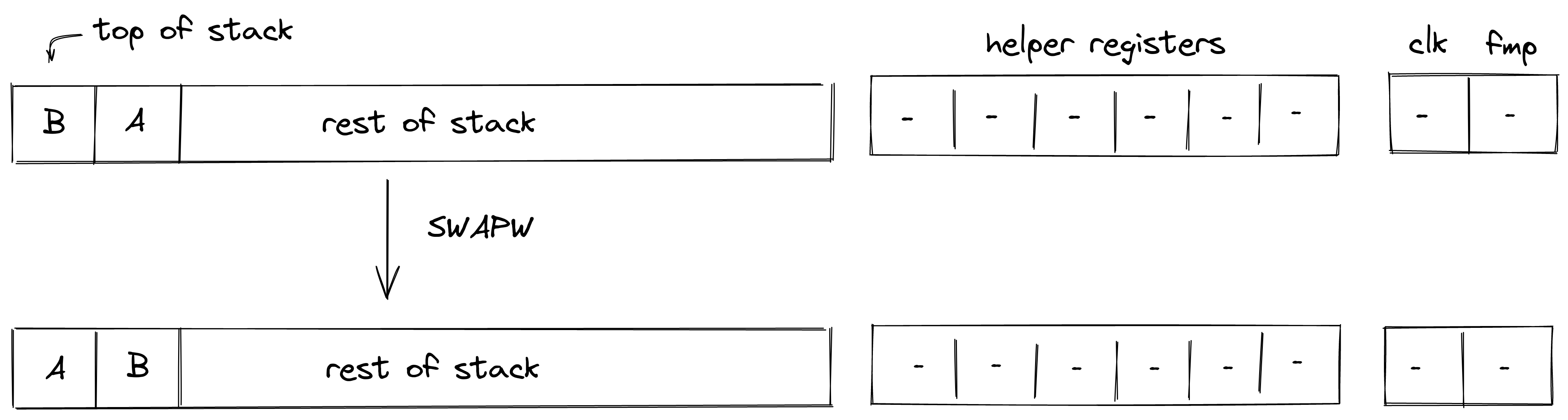
Stack transition for this operation must satisfy the following constraints:
\[ s_{i}' - s_{i+4} = 0 \text{ for } i \in \{0, 1, 2, 3\} \text{ | degree} = 1 \]\[ s_{i + 4}' - s_i = 0 \text{ for } i \in \{0, 1, 2, 3\} \text{ | degree} = 1 \]
The effect of this operation on the rest of the stack is:
- No change starting from position \(8\).
SWAPW2¶
The SWAPW2 operation swaps stack elements \(0, 1, 2, 3\) with elements \(8, 9, 10, 11\). The diagram below illustrates this graphically.
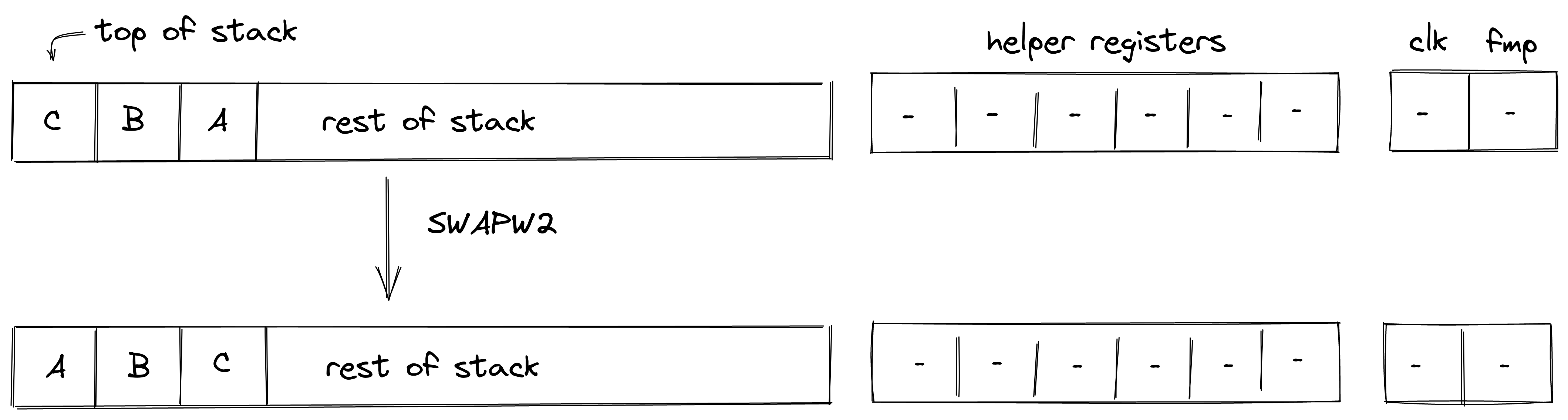
Stack transition for this operation must satisfy the following constraints:
\[ s_i' - s_{i+8} = 0 \text{ for } i \in \{0, 1, 2, 3\} \text{ | degree} = 1 \]\[ s_{i + 8}' - s_i = 0 \text{ for } i \in \{0, 1, 2, 3\} \text{ | degree} = 1 \]
The effect of this operation on the rest of the stack is:
- No change for elements \(4, 5, 6, 7\).
- No change starting from position \(12\).
SWAPW3¶
The SWAPW3 operation swaps stack elements \(0, 1, 2, 3\) with elements \(12, 13, 14, 15\). The diagram below illustrates this graphically.
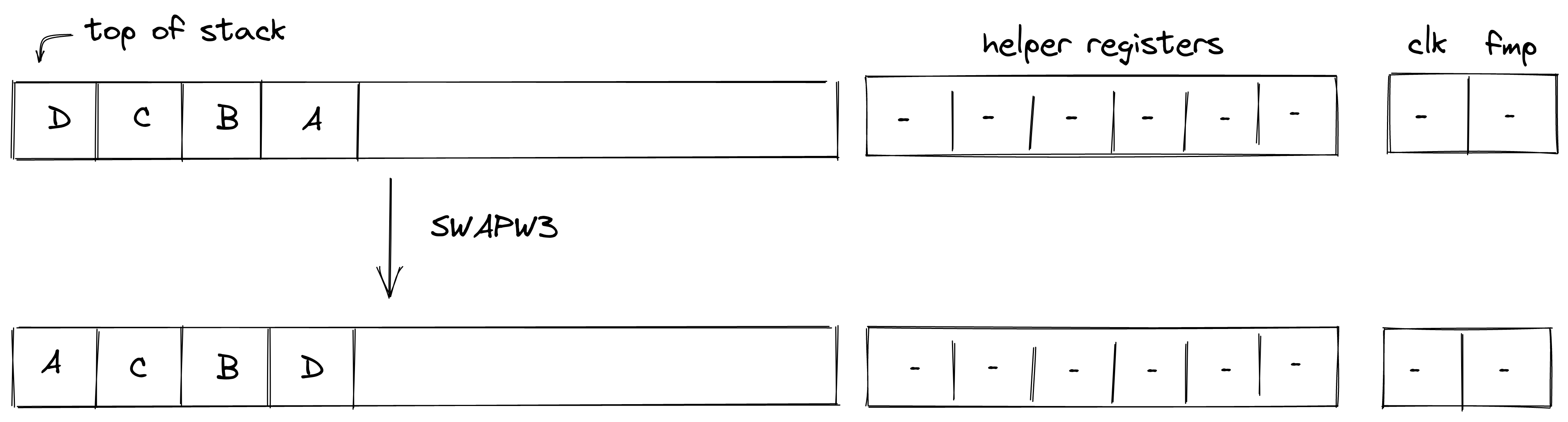
Stack transition for this operation must satisfy the following constraints:
\[ s_i' - s_{i+12} = 0 \text{ for } i \in \{0, 1, 2, 3\} \text{ | degree} = 1 \]\[ s_{i+12}' - s_i = 0 \text{ for } i \in \{0, 1, 2, 3\} \text{ | degree} = 1 \]
The effect of this operation on the rest of the stack is:
- No change for elements \(4, 5, 6, 7, 8, 9, 10, 11\).
- No change starting from position \(16\).
SWAPDW¶
The SWAPDW operation swaps stack elements \([0, 8)\) with elements \([8, 16)\). The diagram below illustrates this graphically.
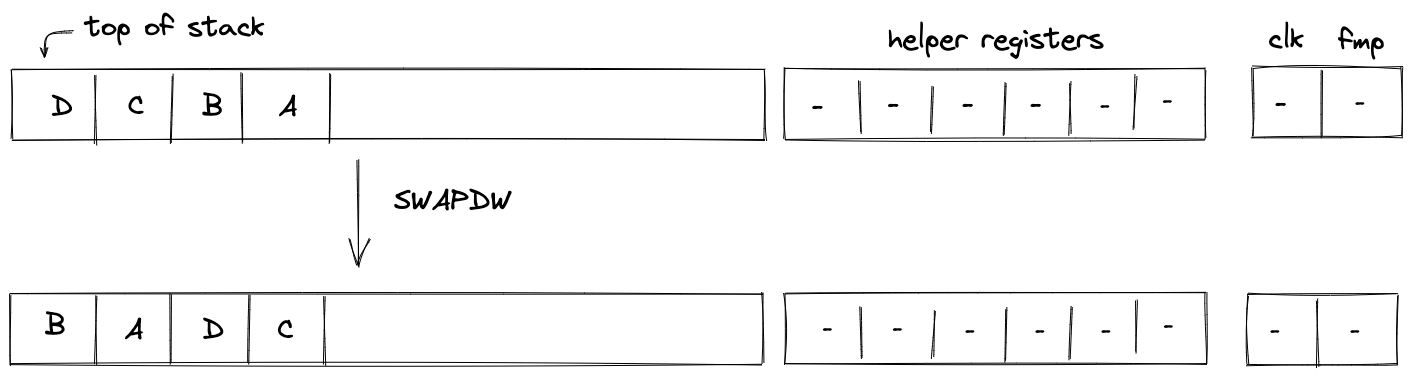
Stack transition for this operation must satisfy the following constraints:
\[ s_i' - s_{i+8} = 0 \text{ for } i \in [0, 8) \text{ | degree} = 1 \]\[ s_{i+8}' - s_i = 0 \text{ for } i \in [0, 8) \text{ | degree} = 1 \]
The effect of this operation on the rest of the stack is:
- No change starting from position \(16\).
MOVUP(n)¶
The MOVUP(n) operation moves the \(n\)-th element of the stack to the top of the stack. For example, MOVUP2 moves element at depth \(2\) to the top of the stack. All elements with depth less than \(n\) are shifted to the right by one, while elements with depth greater than \(n\) remain in place, and the depth of the stack does not change. This operation is valid for \(n \in [2, 9)\). The diagram below illustrates this graphically.
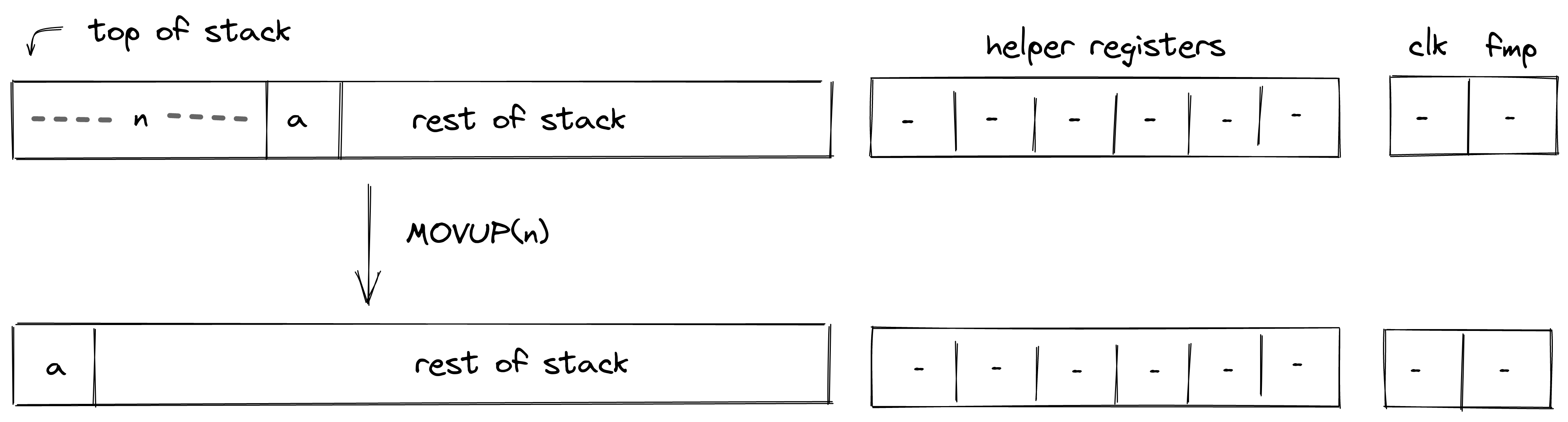
Stack transition for this operation must satisfy the following constraints:
\[ s_0' - s_n = 0 \text{ for } n \in [2, 9) \text{ | degree} = 1 \]
where \(n\) is the depth of the element which is moved moved to the top of the stack.
The effect of this operation on the rest of the stack is:
- Right shift for elements between \(0\) and \(n-1\).
- No change starting from position \(n+1\).
MOVDN(n)¶
The MOVDN(n) operation moves the top element of the stack to the \(n\)-th position. For example, MOVDN2 moves the top element of the stack to depth \(2\). All the elements with depth less than \(n\) are shifted to the left by one, while elements with depth greater than \(n\) remain in place, and the depth of the stack does not change. This operation is valid for \(n \in [2, 9)\). The diagram below illustrates this graphically.
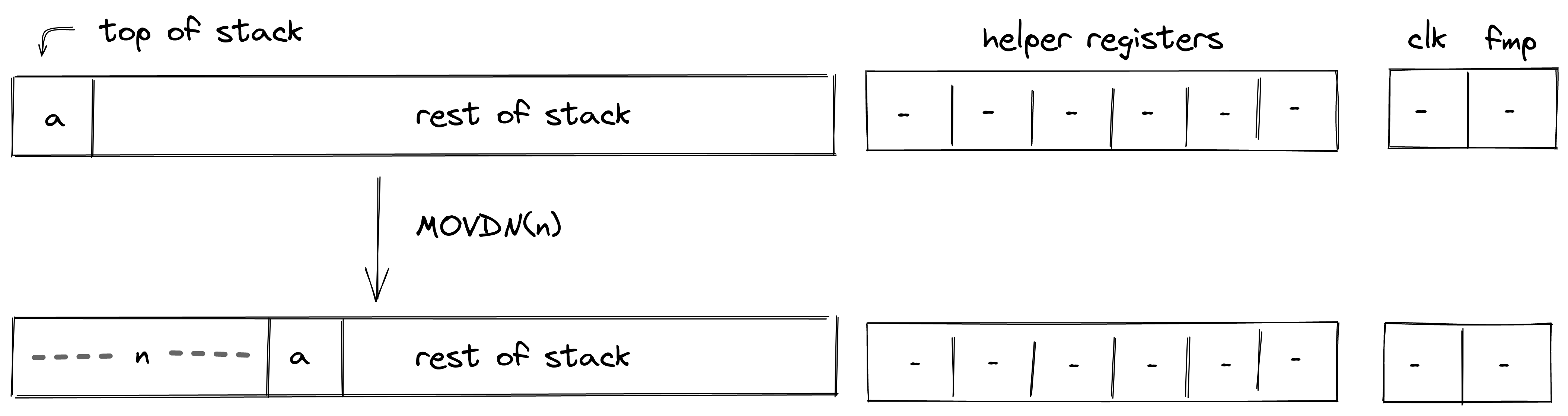
Stack transition for this operation must satisfy the following constraints:
\[ s_n' - s_0 = 0 \text{ for } n \in [2, 9) \text{ | degree} = 1 \]
where \(n\) is the depth to which the top stack element is moved.
The effect of this operation on the rest of the stack is:
- Left shift for elements between \(1\) and \(n\).
- No change starting from position \(n+1\).
CSWAP¶
The CSWAP operation pops an element off the stack and if the element is \(1\), swaps the top two remaining elements. If the popped element is \(0\), the rest of the stack remains unchanged. The diagram below illustrates this graphically.
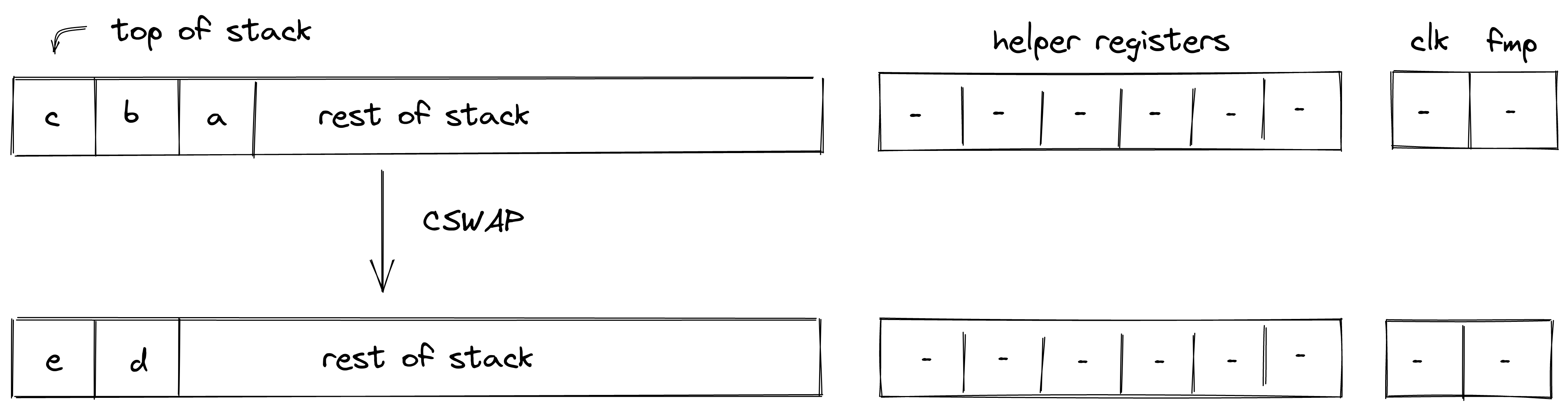
In the above:
Stack transition for this operation must satisfy the following constraints:
\[ s_0' - s_{0} \cdot s_{2} - (1-s_0) \cdot s_1 = 0 \text{ | degree} = 2 \]\[ s_1' - s_0 \cdot s_{1} - (1-s_0) \cdot s_2 = 0 \text{ | degree} = 2 \]
We also need to enforce that the value in \(s_0\) is binary. This can be done with the following constraint:
\[ s_0^2 - s_0 = 0 \text{ | degree} = 2 \]
The effect of this operation on the rest of the stack is: * Left shift starting from position \(3\).
CSWAPW¶
The CSWAPW operation pops an element off the stack and if the element is \(1\), swaps elements \(1, 2, 3, 4\) with elements \(5, 6, 7, 8\). If the popped element is \(0\), the rest of the stack remains unchanged. The diagram below illustrates this graphically.
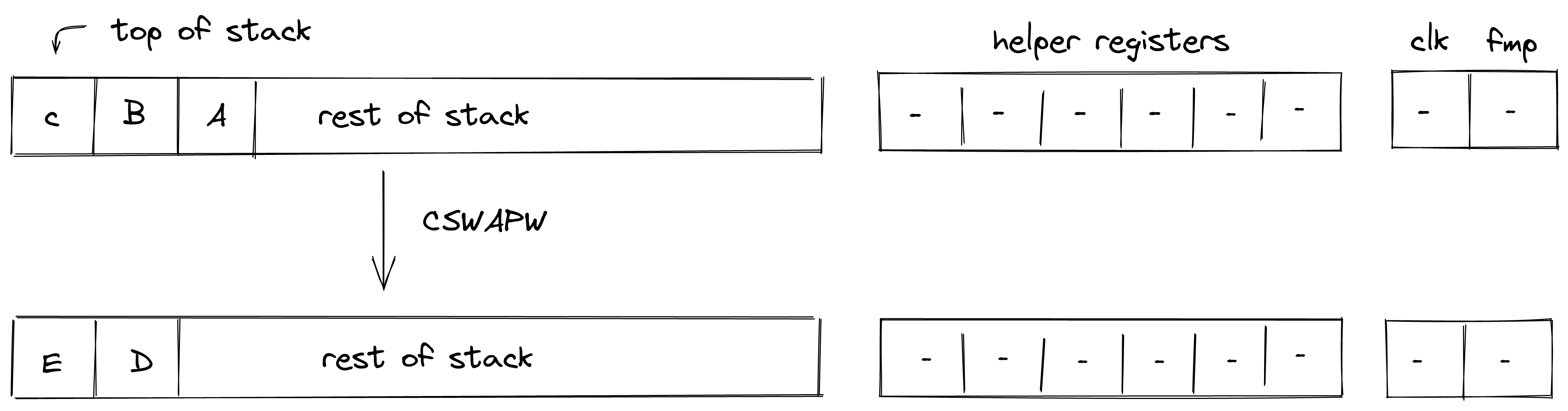
In the above:
Stack transition for this operation must satisfy the following constraints:
\[ s_i' - s_0 \cdot s_{i+5} - (1-s_0) \cdot s_{i+1} = 0 \text{ for } i \in [0, 4) \text{ | degree} = 2 \]\[ s_{i+4}' - s_0 \cdot s_{i+1} - (1-s_0) \cdot s_{i+5} = 0 \text{ for } i \in [0, 4) \text{ | degree} = 2 \]
We also need to enforce that the value in \(s_0\) is binary. This can be done with the following constraint:
\[ s_0^2 - s_0 = 0 \text{ | degree} = 2 \]
The effect of this operation on the rest of the stack is:
- Left shift starting from position \(9\).